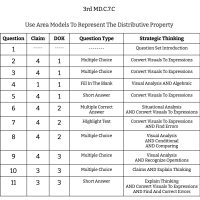
3rd Grade Math - MD.C.7.C - Use Area Models To Represent The Distributive Property
11 Questions
Use Area Models To Represent The Distributive Property Introduction
Each square in the figure below has an area of 1 square unit. We can break the figure into two parts.
Which figure below represents the expression (3 x 1) + (3 x 2)?
Use the distributive property to find the missing factor. Type in your answer.
Use the distributive property to write an expression that represents the area of the figure below. Type in the expression.
Which TWO of the expressions below could represent the area of the figure?
Serena tried using the distributive property to find the area of the figure below, however, she made an error. Click on the step where she made the first error.
Which of the area models below meets the following conditions?
Which of the following word problems could be represented by the image below?
Enrique claims that an array with a width of 1 cannot be modeled with the distributive property. Do you support Enrique's claim? Explain.
Does the expression below and the model match one another? Explain.
We help districts in California boost CAASPP Math Scores by Δ +20% by helping teachers determine if students are struggling with the content, the technology involved with the type of question, or the type of strategic thinking required. Based on the 8 Standards for Mathematical Practice, our platform and professional development empowers teachers to recognize all 16 types of strategic thinking across any math question, curriculum, or assessment.
Learn more