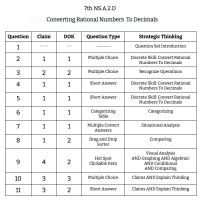
7th Grade Math - NS.A.2.D - Converting Rational Numbers To Decimals
11 Questions
Converting Rational Numbers Into Decimals Introduction
Convert this fraction into a decimal.
Solve the problem below.
Convert the fraction below into a decimal. Round your answer to the thousandths place.
Type in any fraction that produces a repeated decimal.
Which of the decimals below would be considered terminating and which would be repeating?
Which of the fractions below will yield a repeating decimal? Select ALL that apply.
Analyze each of the numbers below and put them in order from least to greatest.
Replace n with any number between -10 and 10 that would meet the following criteria. Place your answer upon the number line.
Jolie states that if a fraction becomes a repeating decimal, then its reciprocal always terminates at or before the number reaches the thousandths place.
Lemuel claims that only fractions with odd number denominators produce repeating decimals. Do you agree with Lemuel? Why or why not?
The question sets found here work best in conjunction with the Strategic Thinking in Math training for grades 1 - 8.
Learn more